Retour à l’article

Démonstration de la formule de calcul des mensualités d’un crédit immobilier:

Formule

Soit: $t_a$ le taux annuel, t le taux mensuel du crédit, C le capital à rembourser, M la mensualité, N le nombre de mois que dure le crédit.

t=ta12{\color{green}t}=\frac{t_a}{12}
M=C×t1−(1+t)−NM=\frac{{\color{red}C} \times {\color{green}t}}{1-(1+{\color{green}t})^{\color{blue}-N}}

Démonstration

Bien que les notions utilisées fassent partie de programme de terminale scientifique le nombre important de variables correspond davantage à un niveau universitaire.

 On note:

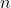  • n le nombre de mois écoulés,
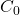  • C0 le capital de départ (il est égal à C )
  • N le nombre total de mois
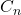  • Cn le capital restant à rembourser au bout de 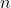n mois
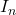  • In le montant des intérêts pour le 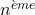n ème mois (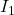I1 est le premier terme de cette suite)

Au bout d’1 mois:

Intérêts: $I_1=C_o \times t$

Montant remboursé: $M-C_o \times t$

Capital restant à rembourser:

$C_1=C_0-(M-C_o \times t)$

Au bout de 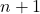$n+1$ mois:

Intérêts: $I_{n+1}=C_n \times t$

Montant remboursé: $M-C_n \times t$

Capital restant à rembourser:

$C_{n+1}=C_n-(M-C_n \times t)$

$C_{n+1}=C_n-M+C_n \times t)$

$C_{n+1}=(1+t) \times C_n-M$

$C_n$ est une suite de la forme $C_{n+1}=aC_n+b$ avec $a=1+t$ et $b=-M$ (suite arithmético-géométrique).

Je cherche donc $x$ tel que:    $x=(1+t)x-M$ 

                                              $x=x+tx-M$

                                              $x=\frac{M}{t}$

Je note $V_n$ la suite telle que $V_n=C_n-\frac{M}{t}$

Vn+1Vn\frac{V_{n+1}}{V_n}
=Cn+1−MtCn−Mt=\frac{C_{n+1}-\frac{M}{t}}{C_n-\frac{M}{t}}
=tCn+1−MtCn−M=\frac{tC_{n+1}-M}{tC_n-M}
=t((1+t)Cn−M)−MtCn−M=\frac{t((1+t)C_n-M)-M}{tC_n-M}
=tCn+t2Cn−tM−MtCn−M=\frac{tC_n+t^2C_n-tM-M}{tC_n-M}
=t(tCn−M)+tCn−MtCn−M=\frac{t(tC_n-M)+tC_n-M}{tC_n-M}
=(t+1)(tCn−M)tCn−M=\frac{(t+1)(tC_n-M)}{tC_n-M}
=t+1=t+1

$V_n$ est une suite géométrique de raison $1+t$ et de premier terme $C-\frac{M}{t}$ donc $V_n=(C-\frac{M}{t})(1+t)^n$

Cn=Vn+MtC_n=V_n+\frac{M}{t}
Cn=(C−Mt)(1+t)n+MtC_n=(C-\frac{M}{t})(1+t)^n+\frac{M}{t}
In=Cn−1×tI_n=C_{n-1} \times t
In=((C−Mt)(1+t)n−1+Mt)tI_n=((C-\frac{M}{t})(1+t)^{n-1}+\frac{M}{t})t
In=(Ct−M)(1+t)n−1+MI_n=(Ct-M)(1+t)^{n-1}+M

Si on ajoute tous les intérêts au capital on obtient le total de toutes les mensualités.

C+∑i=1NIn=M×NC+\sum_{i=1}^N{I_n}=M \times N
C+∑i=1N((Ct−M)(1+t)n−1+M)=M×NC+\sum_{i=1}^N{((Ct-M)(1+t)^{n-1}+M)}=M \times N
C+∑i=1N(Ct−M)(1+t)n−1+∑i=1NM=M×NC+\sum_{i=1}^N{(Ct-M)(1+t)^{n-1}+\sum_{i=1}^N{M}}=M \times N
C+∑i=1N(Ct−M)(1+t)n−1+∑i=1NM=M×NC+\sum_{i=1}^N{(Ct-M)(1+t)^{n-1}+\sum_{i=1}^N{M}}=M \times N
C+(Ct−M)∑i=1N(1+t)n−1+M×N=M×NC+(Ct-M)\sum_{i=1}^N{(1+t)^{n-1}+M \times N}=M \times N
C+(Ct−M)∑i=1N(1+t)n−1=0C+(Ct-M)\sum_{i=1}^N{(1+t)^{n-1}}=0

J’utilise la formule de la somme des $n-1$ premier termes d’une suite géométrique pour la suite de premier terme 1 et de raison $1+t$.

C+(Ct−M)1−(1+t)N1−(1+t)=0C+(Ct-M)\frac{1-(1+t)^N}{1-(1+t)}=0
C+(Ct−M)1−(1+t)N−t=0C+(Ct-M)\frac{1-(1+t)^N}{-t}=0
−Ct+(Ct−M)(1−(1+t)N)=0-Ct+(Ct-M)(1-(1+t)^N)=0
−Ct+Ct−Ct(1+t)N−M(1−(1+t)N)=0-Ct+Ct-Ct(1+t)^N-M(1-(1+t)^N)=0
−Ct(1+t)N+M((1+t)N−1)=0-Ct(1+t)^N+M((1+t)^N-1)=0
M=Ct(1+t)N(1+t)N−1M=\frac{Ct(1+t)^N}{(1+t)^N-1}
M=Ct(1+t)N(1+t)N(1−1(1+t)N)M=\frac{Ct(1+t)^N}{(1+t)^N(1-\frac{1}{(1+t)^N})}
M=Ct1−1(1+t)NM=\frac{Ct}{1-\frac{1}{(1+t)^N}}
M=Ct1−(1+t)−NM=\frac{Ct}{1-(1+t)^{-N}}

Démonstration de la formule de calcul des mensualités d’un crédit immobilier